Compute the Right Sibling Tree

Extended Binary Tree Functionality

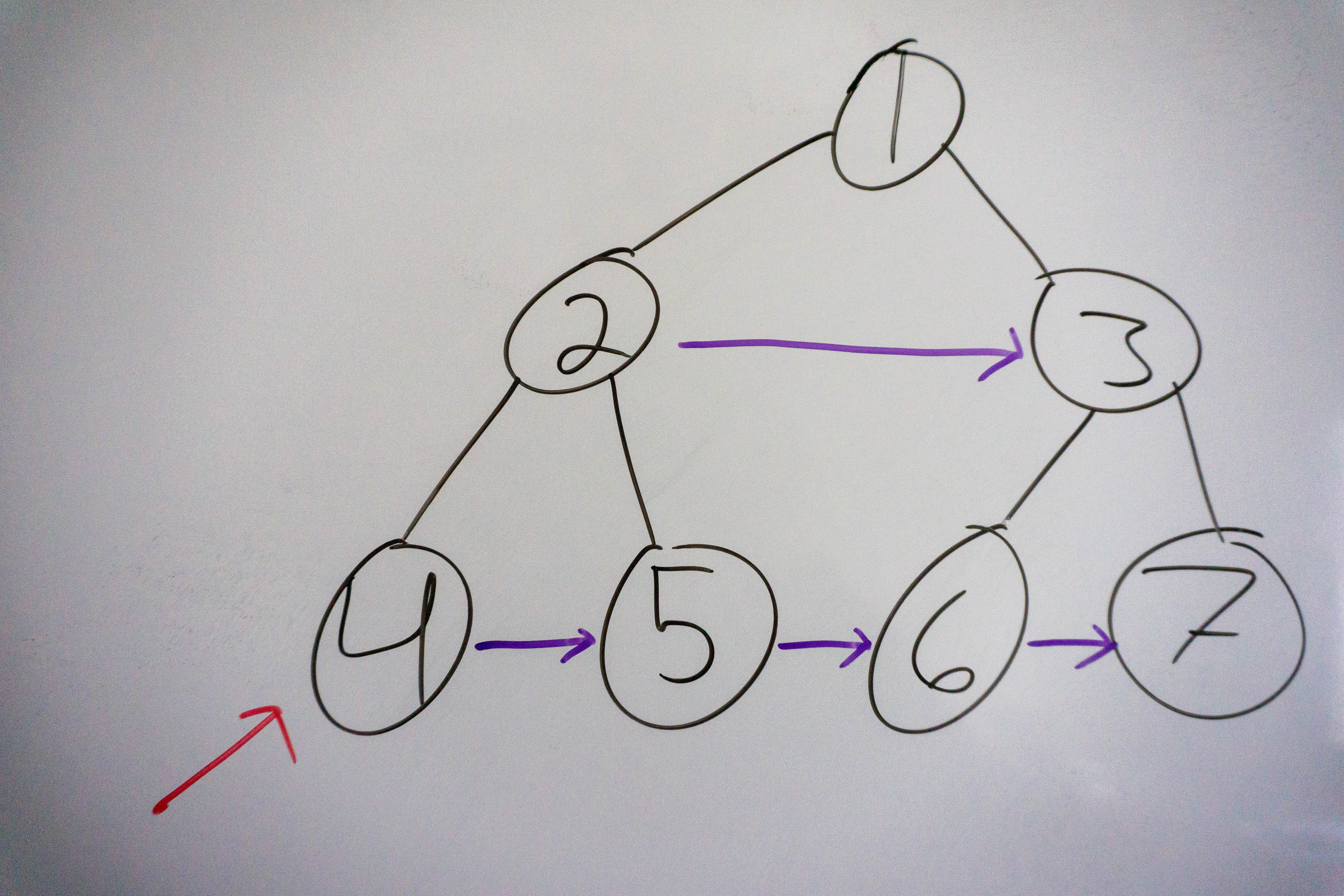
The beautiful thing about data structures is that they turn seemingly basic objects such as arrays and lists into powerful tools that can be used to solve a multitude of problems. Consider the array, which in its most basic implementation can be used to store and retrieve objects at a certain position. However, add a few pointer and a couple methods and suddenly we have a stack, or a heap, or even a queue. There’s also no limit to the different types of custom classes we can create to fit any number of scenarios. Today, we are going to extending the class binary tree by adding an additional property to it. We will be adding a new property called right, which points to the node’s next right node. The next right node is the next node that can be found to the right of the current node on the same level. Take a look at the tree below to understand how this pointer works:

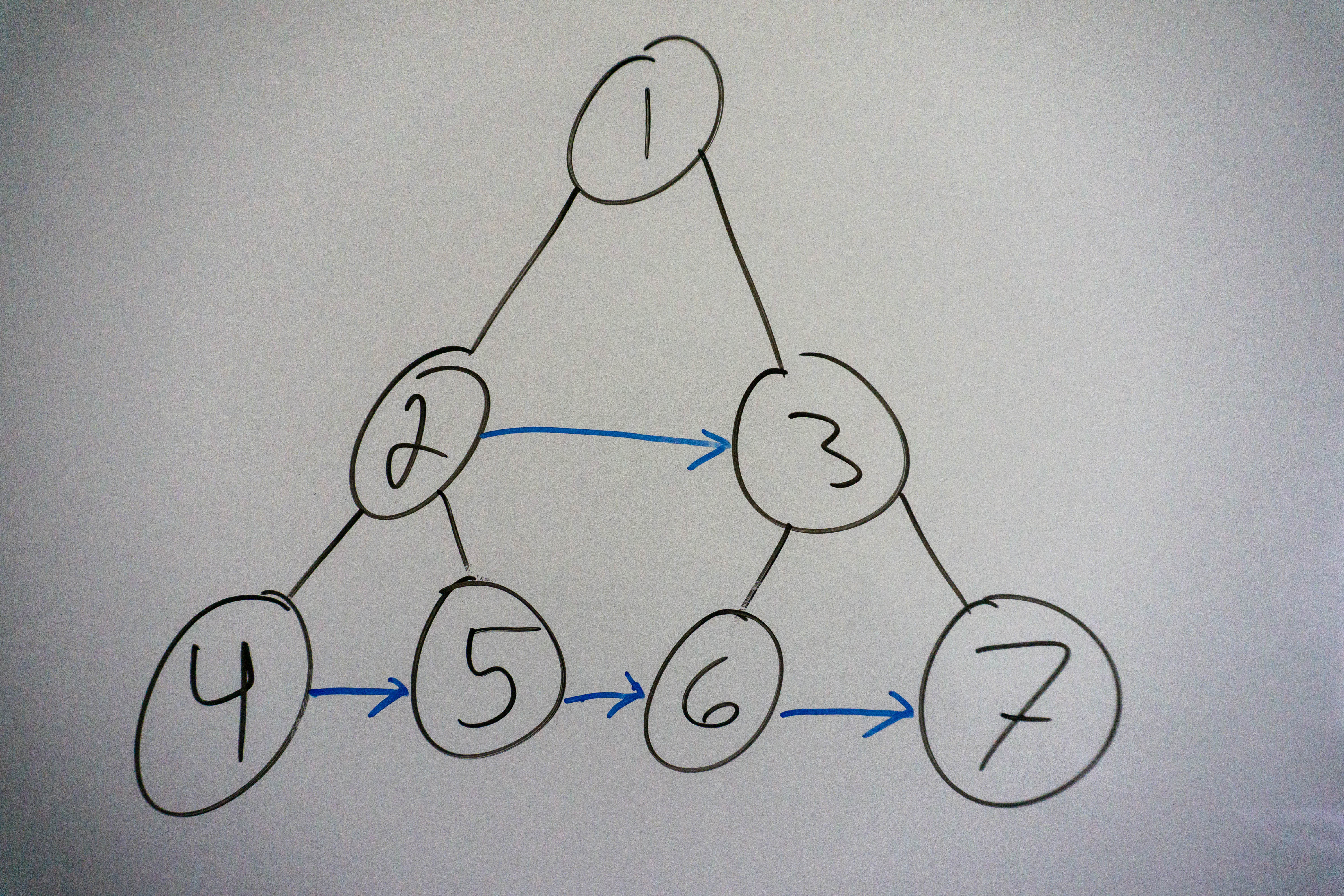
2 has a right pointer to 3. 4 has a right pointer to 5, which has a right pointer to 6, which has a right pointer to 7.

Our goal will be to take a given perfect binary tree (more on perfect binary tree here, one in which all right pointers are set to null, and update all the right pointers to point to the correct node. Furthermore, we will also be doing this in O(1) extra space, excluding the space needed for the call stack. I originally stumbled upon this problem in Elements of Programming Interviews page 144, it can also be found on leetcode here. Without further ado let’s begin!

Initial Impression

Before we start writing code it’s important we consider the information we have available to us and the goal we would like to achieve. We are given the root of a perfect binary tree in which we will have to update the right pointer of each node. “Update the right pointer of each node”, that phrase tells us what we have to do and gives us a launching off point to begin pondering solutions. The first thing we should consider is how can we update the right pointer of a certain node in a tree? Looking at the tree above in if we wanted to update the right pointer of 2 to point to 3, how do we do that? Clearly we cannot update the pointer if we were at 2, since 2 does not know about the other nodes on its level, it only knows about its children. That is going to be our first hint for solving this problem, that a node on level i will set the right pointers of its children on level i + 1. After the current node updates the pointers of its children what should it do next? Take a look at the tree below to help visualize the current state of the tree:

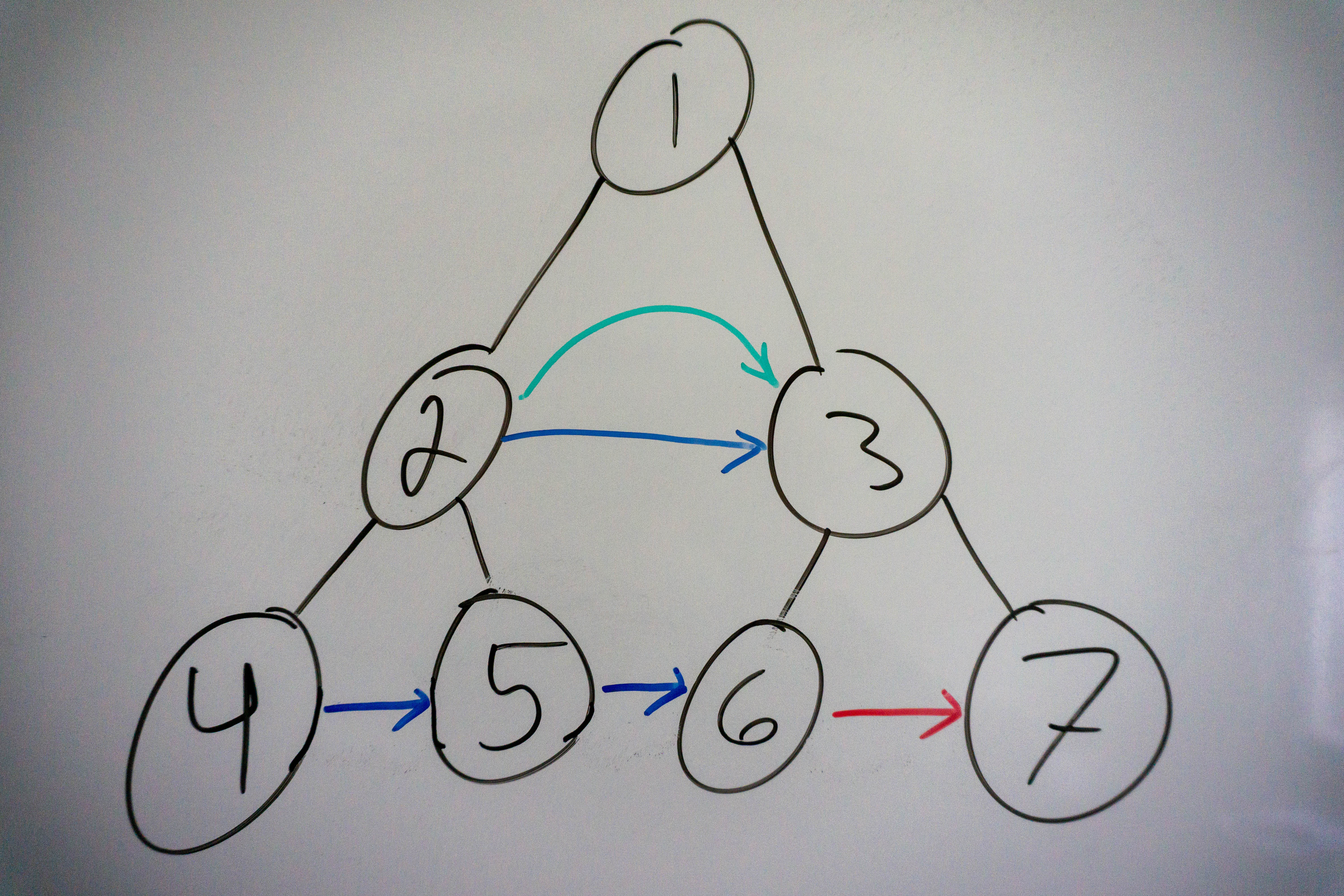
As you can see 2 just set the right pointer for nodes 4 and 5, we need to move to 3 to see the right pointers for 6 and 7. Assuming our algorithm worked correctly when it began at 1, we know that 2 contains a right pointer for 3. With this we can “leap” across the tree, to the next node that should set the pointer for this level. We continue leaping across the nodes until we reach the right most node, this node’s right pointer will be null, so we can use that to know when it’s time to move own to the next level. Let’s quickly summarise the information above:

• Beginning from the root we set the right pointers for the left and right children
• We traverse each level going from left to right, crossing the “gap” between subtrees using the right pointer of the current node
• We are finished on a level when we reach a node that has a null right pointer

An Iterative Solution

Now that we have a general idea of how to solve this problem lets start coding up a solution. We are going to implement an iterative solution for this problem, moving down the tree by following the left most node each time. Since we want to cover all node in a level going from right to left we will traverse down the tree by moving to the left child each time. Let’s code our first function that will “bootstrap” our solution:

    public Node Connect(Node root) {
        if(root == null){
            return root;
        }
        Node current = root;
        while(current != null){
            SetPointers(current);
            current = current.left;
        }
        return root;
    }

Let’s go to the whiteboard to see how this iteration will proceed: 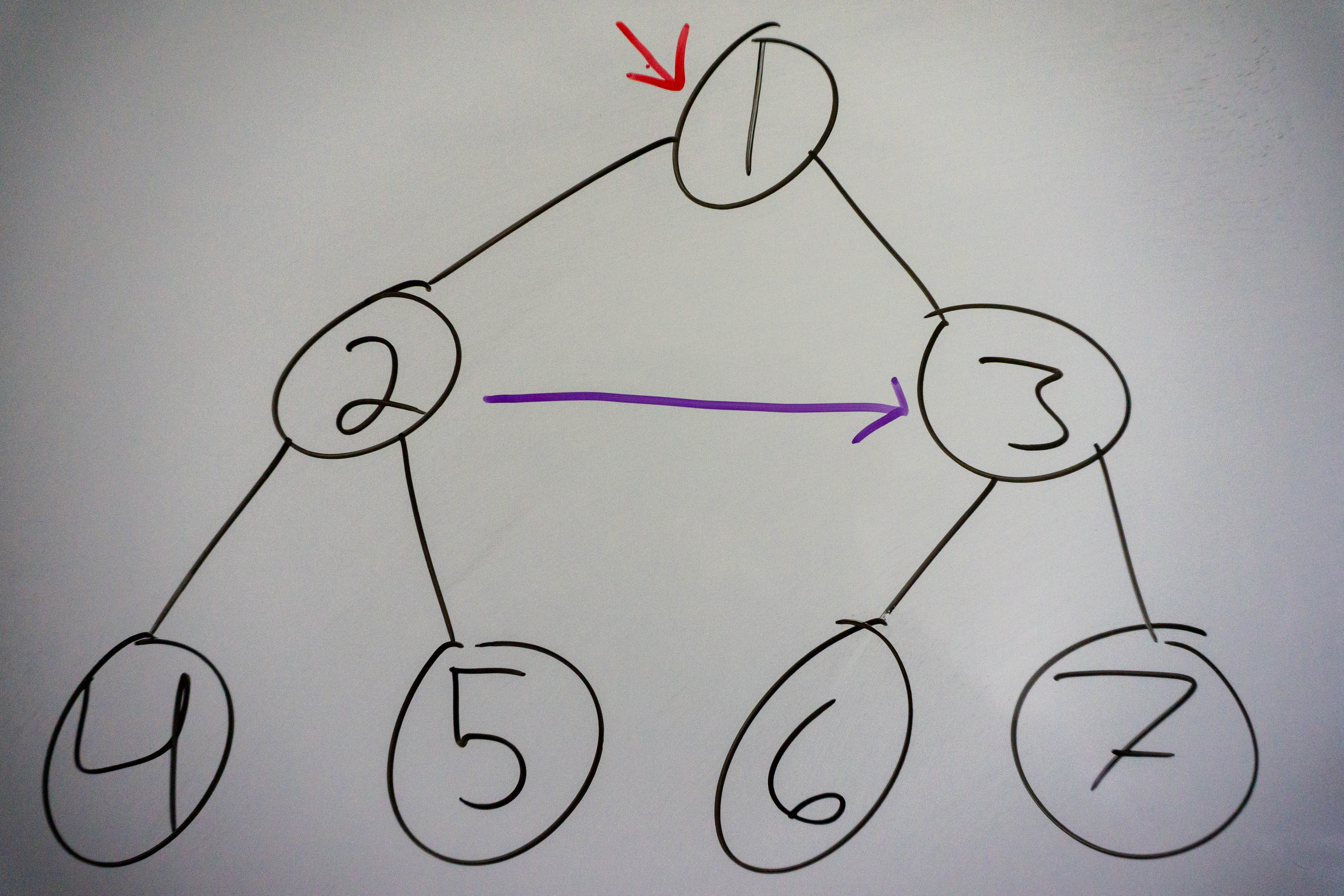Start at the root and move to the left child

Once we are done at the root, move down 1 level to the left child of the current node if it exists, adding the links to each child:

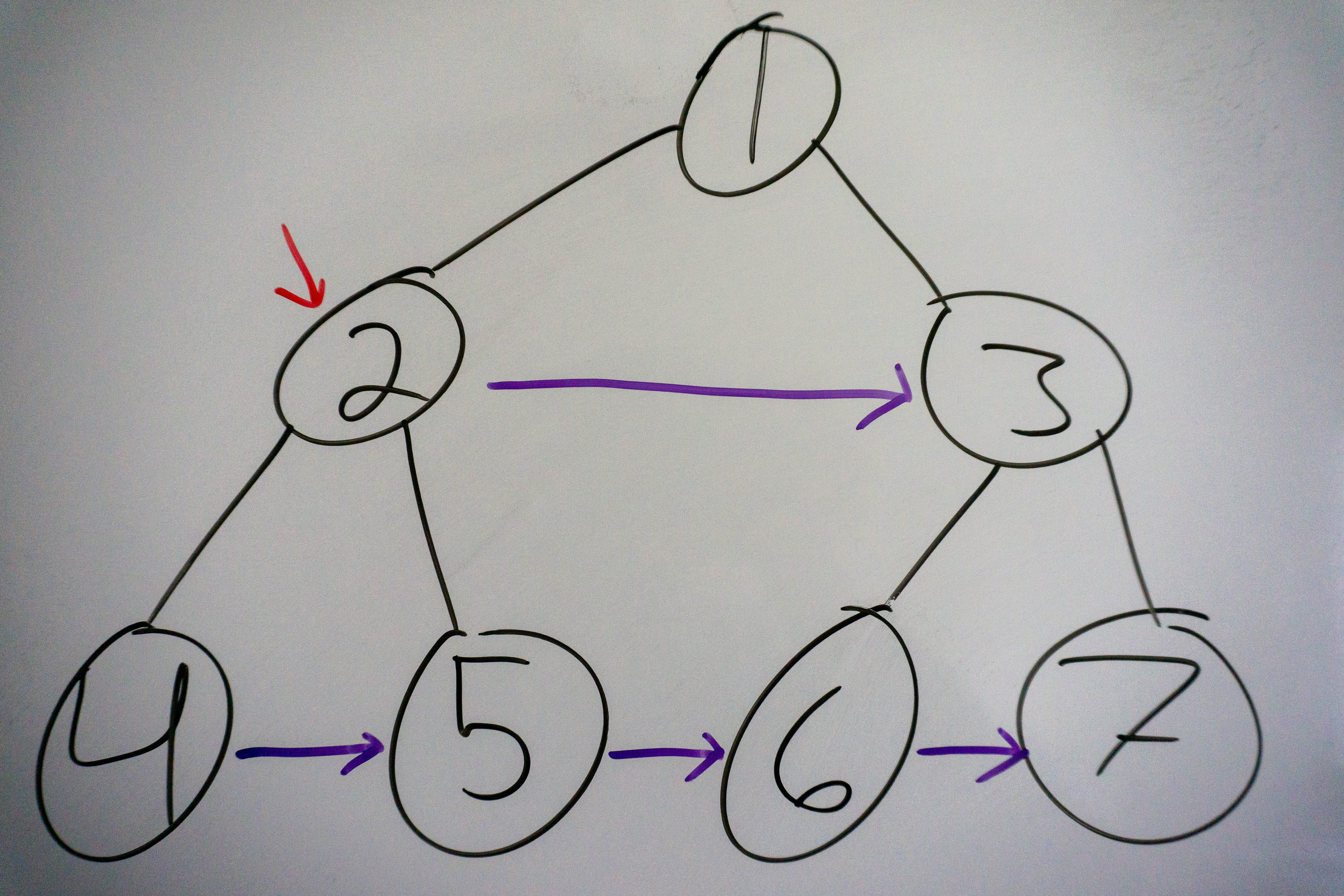
Finally move down to the last level:

Let’s now take a look at the code that will traverse each level and add the links where needed:

    private void SetPointers(Node root){
        while(root != null && root.left != null){
            root.left.next = root.right;
            if(root.next != null){
                root.right.next = root.next.left;
            }
            root = root.next;
        }
    }

The function traverses the level and sets the pointers of the children so long as the current node is not null. We also add the check “root.left != null” because if we are on the last level we don’t have any children nodes to take care of.

Putting this all together our finished class is:

public class Solution {
    public Node Connect(Node root) {
        if(root == null){
            return root;
        }
        Node current = root;
        while(current != null){
            SetPointers(current);
            current = current.left;
        }
        return root;
    }
    private void SetPointers(Node root){
        while(root != null && root.left != null){
            root.left.next = root.right;
            if(root.next != null){
                root.right.next = root.next.left;
            }
            root = root.next;
        }
    }
}

Closing Thoughts

This type of problem can seem complex at first, and at first glance we might assume the solution is equally as complex. However, as we came to see here the solution to these types of problems can be very simple, so long as we take the time to properly analyze and break down the problem into manageable steps. The use of a whiteboard can help us visualize how our solution will run and what it looks like at each step. That’s all for today, stay tuned for more content!