Balanced Binary Trees

Before beginning this post, I just wanted to state that this post was originally supposed to go live yesterday, the 22nd of May, but got delayed to today the 23rd because of issues related to Github. Github services were experiencing problems yesterday, especially Github Pages, thankfully all is resolved now, so here is the post, enjoy!

Balanced Binary Tree

A balanced binary tree is a binary tree in which the height of the left and right subtrees of any node differ by no more than one. Given an arbitrary binary tree how would we determine if it’s balanced or not? This is the problem we are going to tackle today.

This problem is from cracking the coding interview page 110. The problem tasks us with deciding whether a binary tree is balanced or not, based on the conditions stated above. It’s fairly easy to come up with a simple recursive solution to this problem that gets the job done, albeit with some caveats. The ‘obvious’ recursive solution is not very good in terms of time complexity, in fact complexity is O(n^2). A more subtle solution will be presented which will allow us to reduce this time complexity all the way down to O(n), a big improvement!

Before we dive in I want to note that I won’t be discussing binary trees and their specifics here. In the coming days I plan on doing a post where I will talk about binary trees and their properties, so stay on the lookout for that If you’re interested! Anyways, let’s get to work.

A first recursive solution

The first solution we are going to be looking at is a naive recursive solution that runs in O(n^2). I say naive not because the solution is necessarily bad, but simply because it’s slow and we can do better. Don’t feel bad if it’s the first solution that comes to your mind (it was for me), it’s always better to start somewhere and then improve as we go along. It’s very important that we see and understand this solution so that we understand how we can improve it. Our first solution involves starting at our root and then verifying that it is balanced by calculating the height of its left and right subtrees. Then we move onto the left subtree and verify it is balanced and then the right subtree as well. Here is the code for this solution:

        public bool IsBalanced(TreeNode root)
        {
            if(root == null)
            {
                return true;
            }

            int diff = getHeight(root.left) - getHeight(root.right);

            if(Math.Abs(diff) > 1)
            {
                return false;
            }
            else
            {
                return IsBalanced(root.left) && IsBalanced(root.right); 
            }
        }

        public int GetHeight(TreeNode root)
        {
            if(root == null)
            {
                return -1;
            }
            return Math.Max(GetHeight(root.left), GetHeight(root.right)) + 1;
        }

Pause for a moment and think about what’s happening here. To know if the root is balanced we calculate the height of the left and right subtrees, going from top to bottom. How do we calculate their height? By calculating the height of their respective subtrees. We repeat this process till we reach the bottom of the subtree and then return the values upwards. A null node has a depth of -1, each node returns the maximum value of its left and right subtrees + 1. So a leaf node returns a depth of Math.Max(-1,-1) + 1 = 0. The problem here is that once we finish checking the left and right subtrees of the root we move down a level in the tree and repeat the process all over again. We are calculating the same information many, many times.

We are recalculating the same information repeatedly because we approached the problem from a top down perspective, which requires us to deal with the root of the tree and all its subtrees to construct the final solution. Instead of doing that lets flip our thinking around and try a bottom up approach.

A bottom up solution

For the bottom up approach we are going to start at the bottom, at our leaf nodes, and build up our solution once piece at a time before we reach our final goal. We are going to begin with checking our lowest subtrees and then propagate their values upwards. The main idea behind this solution is that by calculating the depths of the lowest subtrees first, we don’t have to recalculate them each time we need to check if a particular subtree is balanced. When we arrive upon a new node, we will already have in our possession the depths of our left and right subtrees, which we can use to calculate our own depth, and then pass that information onwards. We are essentially doing a depth first search of our tree, calculating the height of a node when the recursion finishes. Let’s have a look at the code before we continue:

        public int DFSHeight(TreeNode root)
        {
            if (root == null)
            {
                return -1;
            }
            int leftHeight = DFSHeight(root.left);
            if (leftHeight == int.MinValue)
            {
                return int.MinValue;
            }
            int rightHeight = DFSHeight(root.right);
            if (rightHeight == int.MinValue)
            {
                return int.MinValue;
            }
            int diff = Math.Abs(leftHeight - rightHeight);
            return diff > 1 ? int.MinValue : Math.Max(leftHeight, rightHeight) + 1;

        }

Let’s look at the code line by line and see what’s happening. Just like the first example if our root is null we return we return -1. Next we recursively explore the left hand side of the tree until we reach a leaf node. How do we know our recursion ends on a leaf node? Well, once we reach a leaf node the call to DFSHeight(root.left) will return -1 and so will DFSHeight(root.right). Therefore, our leaf nodes will be sitting atop our call stack. Once we get the height of our left subtree we verify that its value is not equal to int.MinValue; Why is this the case? The last line of our program is essentially saying the following: “if my left and right subtrees differ in depth by more than 1, I will return the minimum integer value, else I will return my depth to the caller”. The reason we check for this value is because if one of our subtrees if unbalanced, then we will be unbalanced as well, a node can only be balanced if both its subtrees are balanced as well. We choose int.MinValue because no other scenario will cause us to return that value, it essentially acts as a flag, alerting us that the subtree is unbalanced. We could have chosen any value, so long as it would not get returned in the case when our subtree is balanced. For example, we wouldn’t want to choose an positive integer such as 1 or 5, because a node of depth 5 will return 5, and we would think it’s unbalanced, when it’s not. We could have also chosen say -2 or -3, because the lowest integer value we return is -1. int.MinValue is chosen because it’s easy to spot and also jumps out at us.

We are propagating the depths of each subtree upwards, while checking for balance at each step. If we become any balanced at any point, then our flag will take precedence at get passed up instead of the depth. This allows us to visit each node only once, giving us an O(n) solution, much improved from our initial solution. Let’s go to the whiteboard to see visualize how this works:

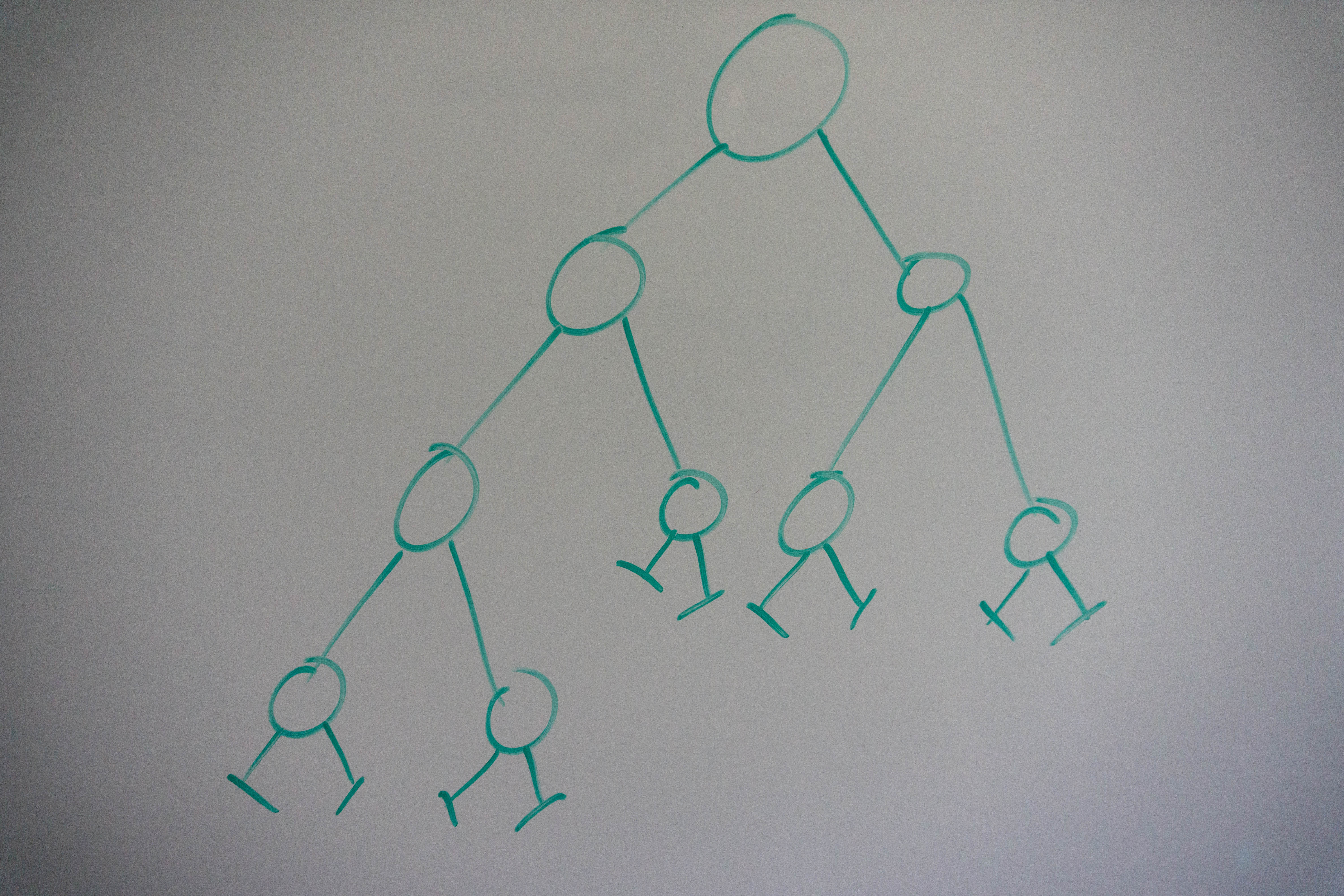Here is the binary tree we are working with, the symbols on the leaf nodes (-|) represent null nodes, which return a value of -1.

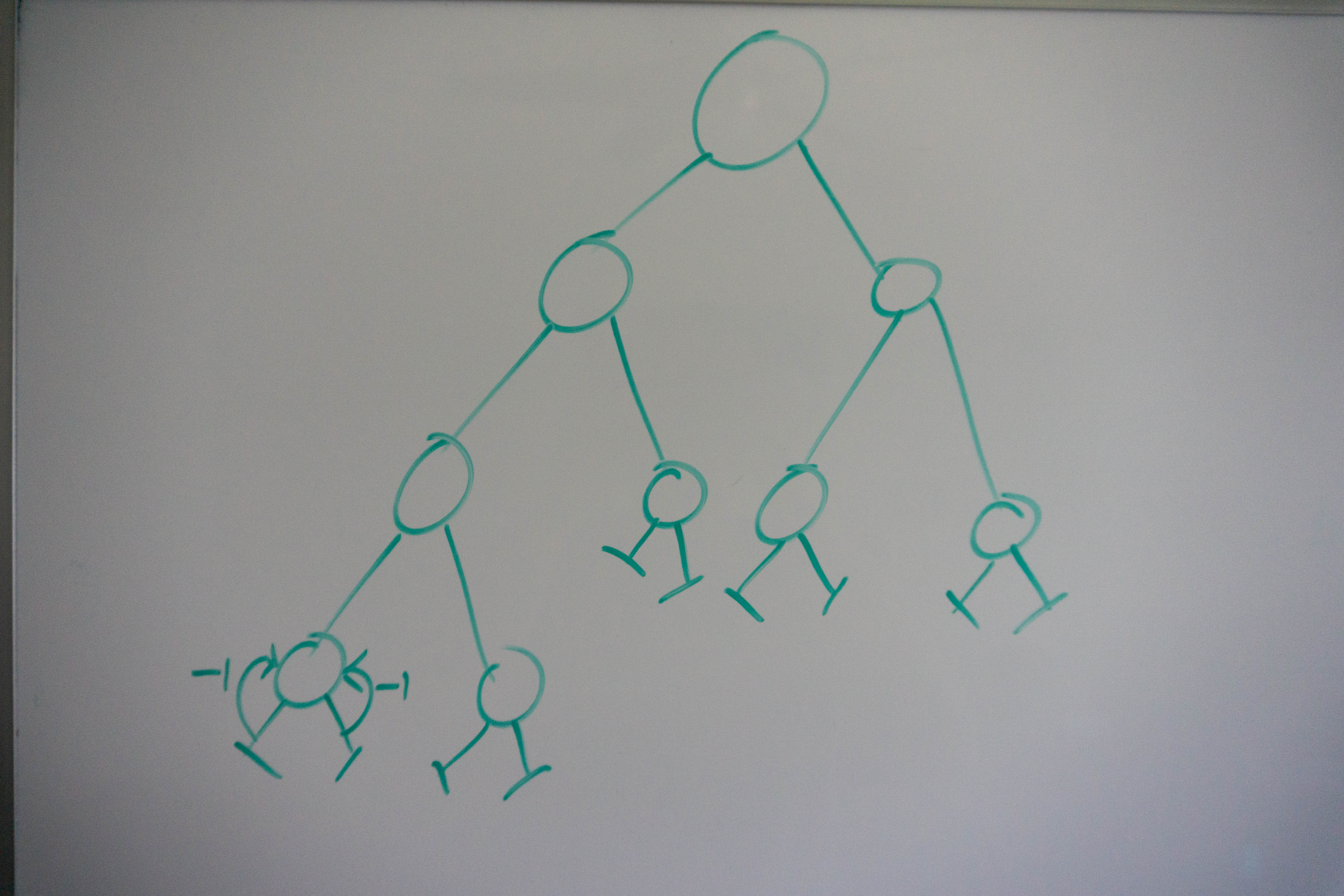We reach our left most leaf node and since it’s a leaf node, its left and right sides return -1.

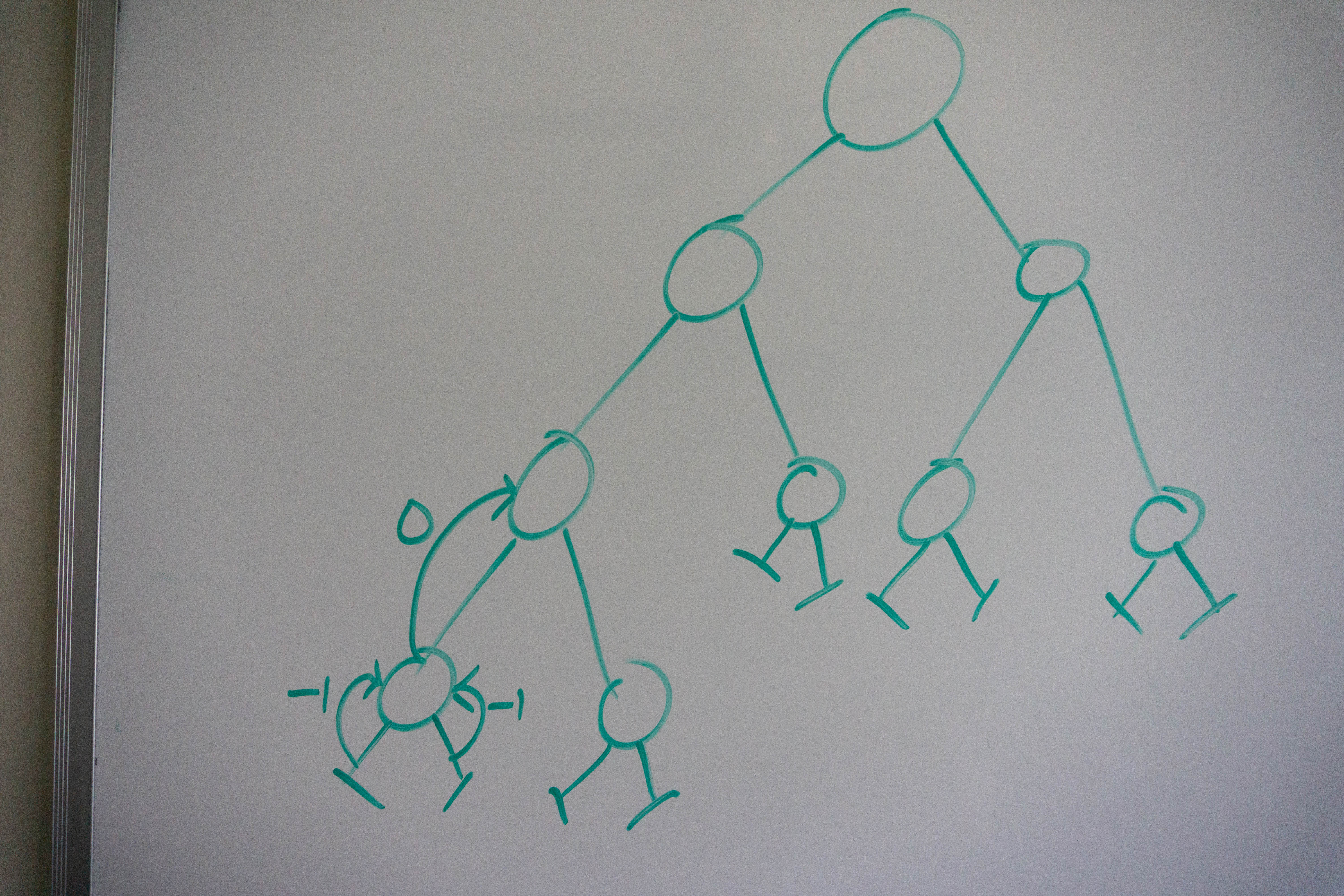This leaf node return the maximum of its two children + 1, which is -1 + 1 = 0.

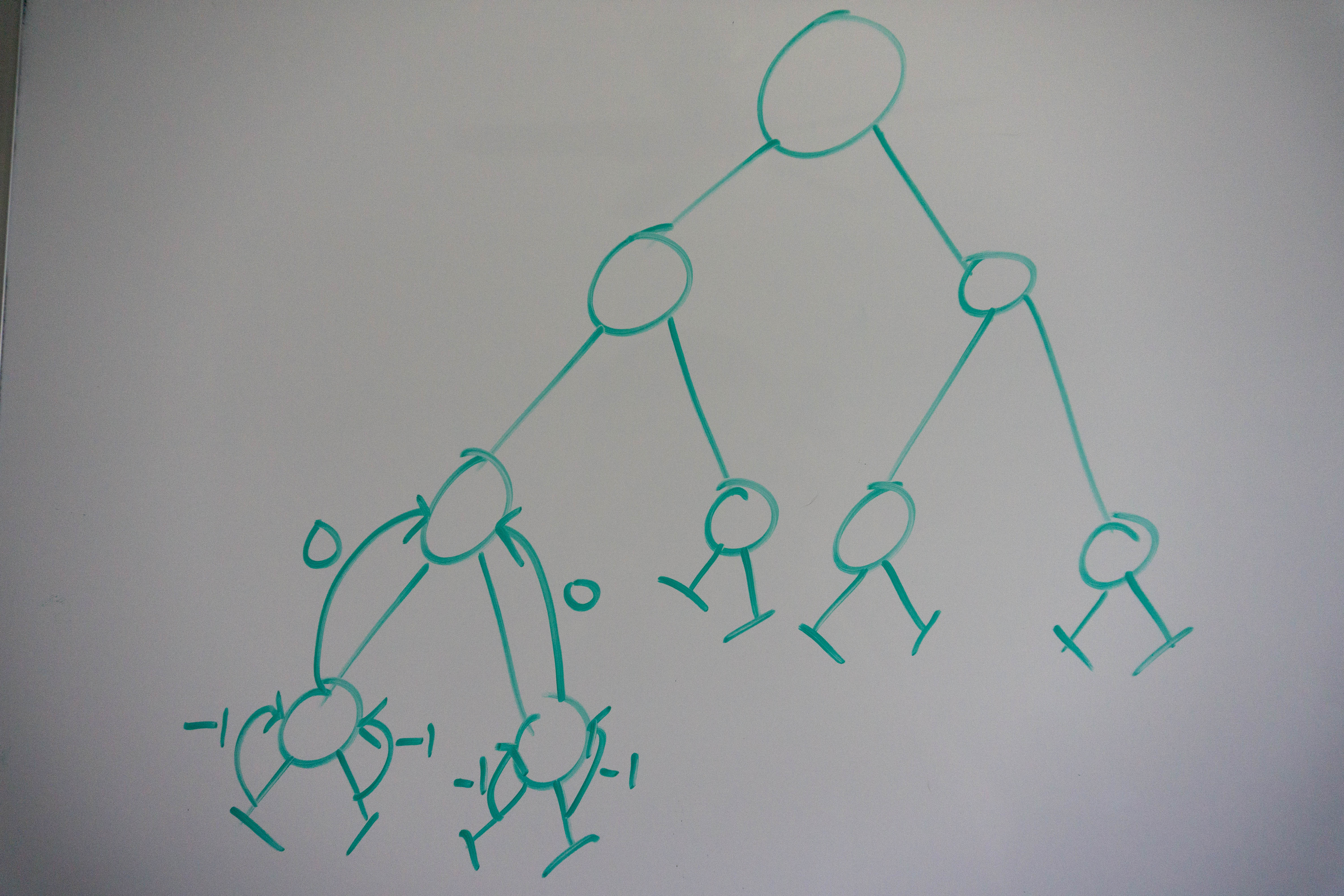We now recurse from the parent node down to the right side. The same thing occurs for the right side as did on the left, which means the right side returns 0.

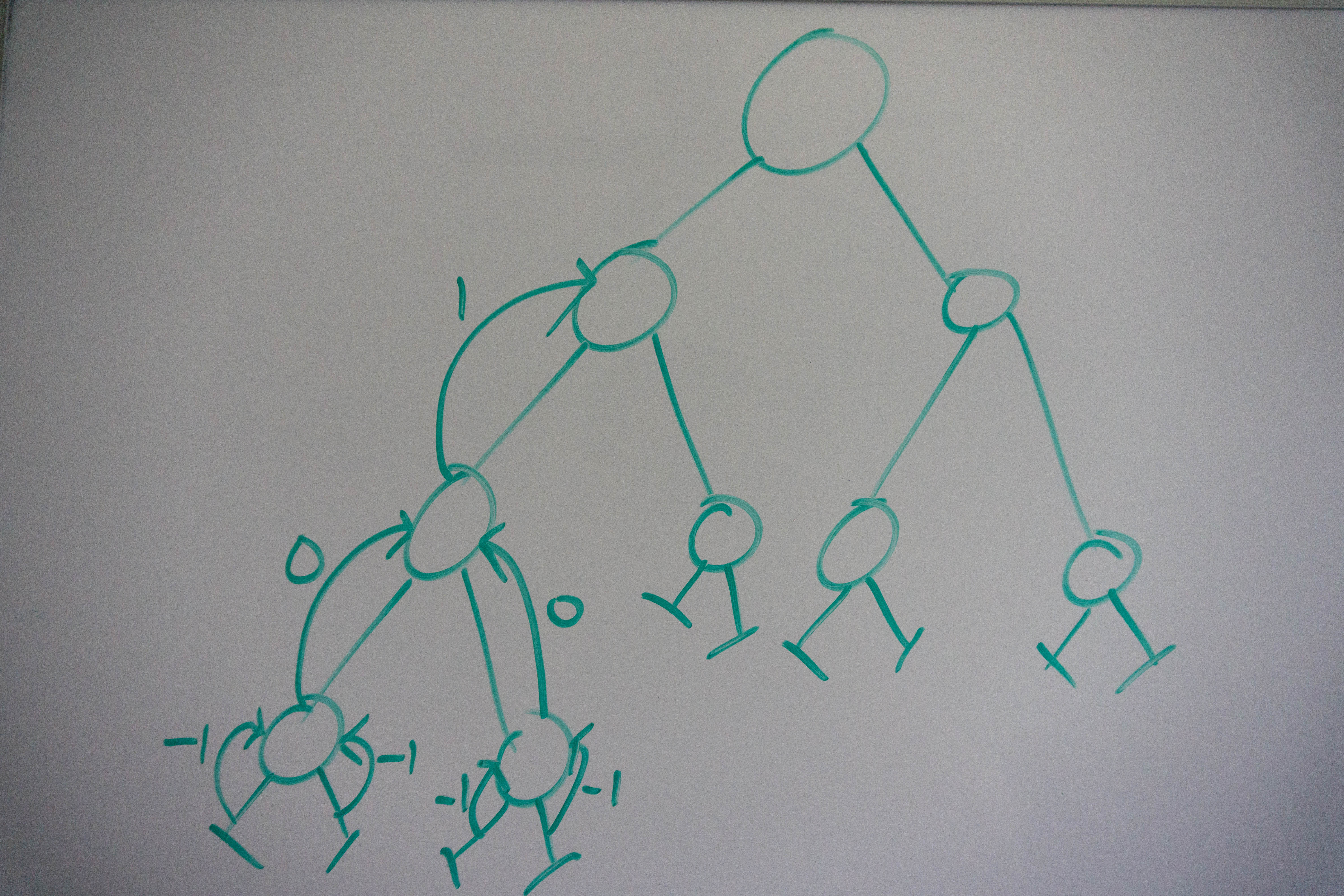The parent node verifies that the left and right subtrees differ in height by no more than 1, which they don’t, and then returns the maximum of its left and right subtrees + 1.

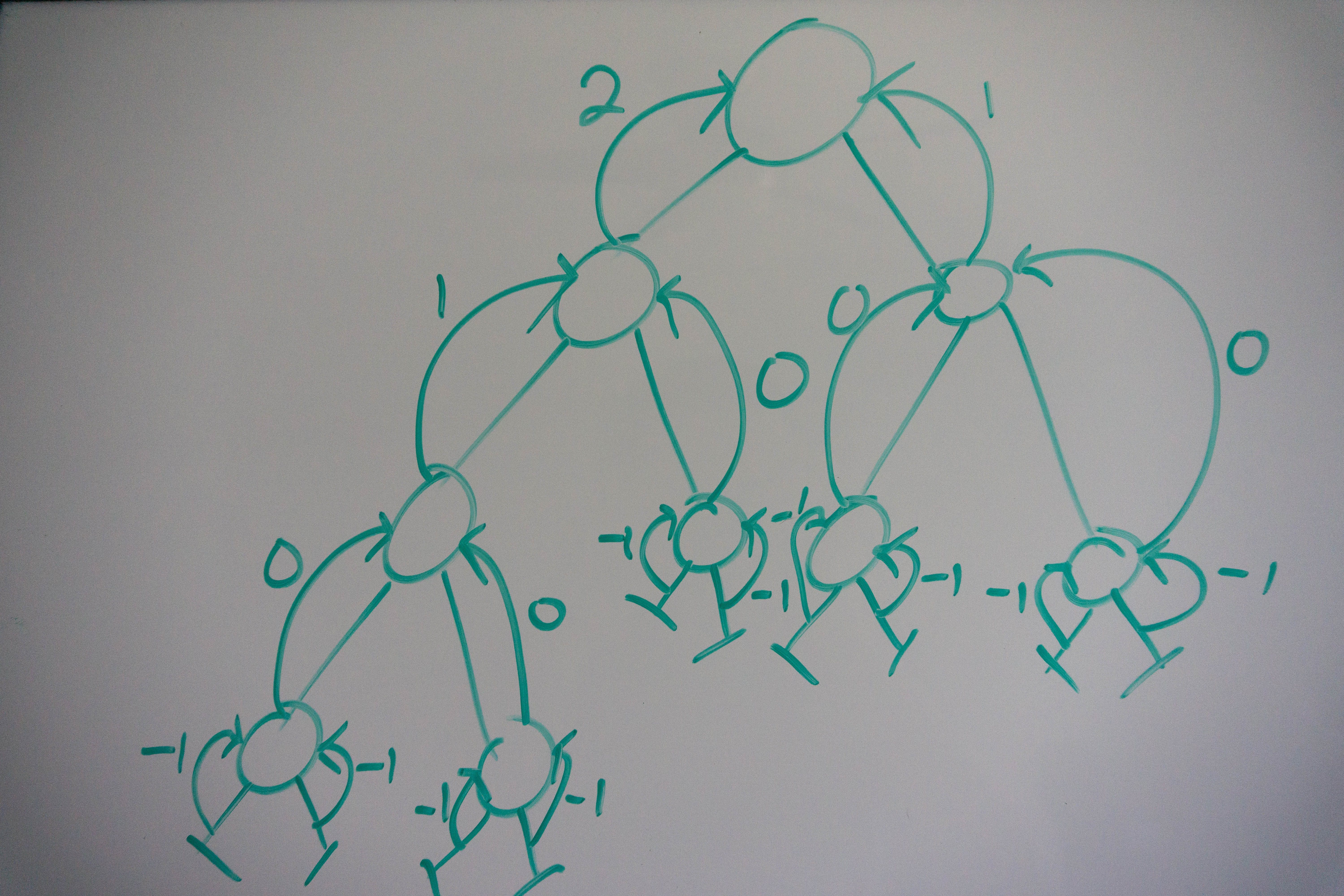Once we reach the root of the entire tree, we recursively check the right subtree, because our left subtree is balanced. The right subtree returns 1, which we then compare with the depth of the left subtree, after verifying the balance we return true.

Above is what happens when we give our algorithm a balanced tree, check out what happens when the tree is unbalanced: Once we discover and unbalanced subtree we stop recursing to our left and right subtrees and propagate the value upwards, all the way to the root. I denote this as passing up negative infinity, or passing up int.MinValue in our code.

The key takeaway here is the concept of propagation, or passing up values. We begin at the bottom of our tree and propagate values upwards, until we reach the root. This concept is extremely useful here because it allows us to visit each node only once, starting from the bottom and passing our answers upwards. It also allows us to propagate errors or flags up as well, so we know the final outcome to our problem. When tackling problems involving binary trees make sure to keep this in mind, as it could be useful for deriving an efficient solution.

Conclusion

There we have it folks! I hope you enjoyed this post on this binary tree problem and then you learned something from it. I’m mulling over starting a new mini series on binary trees, where I would make a small post everyday covering different properties of binary trees, or starting a series on recursion. Either way, keep checking the blog every few days to stay up to date with what I post next. As always, thanks for reading and stay tuned for more content!